Fractal Home
Heeren-Symbol-Algorithmus für Primzahlen
Jeder mathematisch Interessierte hat bereits einmal vom Sieb des Eratosthenes gehört, wenn es um die Bestimmung von Primzahlen geht. Viele andere Verfahren bauen auf Optimierungen dieses Siebs auf. In der höheren Mathematik gibt es algebraische Methoden, um die Suche zu beschleunigen.
Warum nicht einmal ein ganz anderer Ansatz? Birke Heeren hat bereits
2007 einen Symbol-Algorithmus - damals noch mit Papierstreifen und Symbolkarten - entwickelt,
bei dem durch regelmäßige Manipulationen weniger Symbole eine Kette aufgebaut wird, aus der die Lage der
Primzahlpositionen und Lücken in der Menge der natürlichen Zahlen hervorgeht.
Die Motivation ist nicht, mit anderen Verfahren zu konkurrieren, es geht vielmehr um die
Erkundung dieses fraktalen Verteilungsmusters.
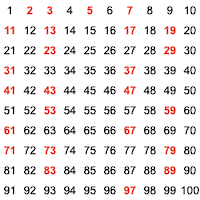
Die Verteilung der Primzahlen
In seinem Buch Die Musik der Primzahlen legt Marcus du Sautoy zu Beginn die Leitfragen fest:
Primzahlverteilung
Primzahlen sind die «Atome» der Arithmetik - nur durch eins und sich selbst teilbar. Gleichzeitig gehören sie zu den quälendsten Geheimnissen der Wissenschaft. 2, 3, 5, 7, ... - lässt sich voraussagen, welches die nächste Primzahl ist? Verbirgt sich hinter dem Rhythmus ihres Auftretens vielleicht ein bestimmtes Muster?
Diese Fragen beschäftigen Forschende seit mehr als 150 Jahren. Wie sind die Primzahlen und die Lücken dazwischen in der Menge der natürlichen Zahlen verteilt?
Auch Birke Heeren hat sich diese Frage gestellt und einen Algorithmus gefunden, bei dem wenige Symbole mit drei Teilprozessen:
● move ● copy ● change
so manipuliert werden, dass sich bei jedem Iterationsschritt Informationen über die Lage weiterer Lücken und Primzahlen aus der gewonnenen Zeichenkette CPn ergeben. Erkunden Sie die Schritte und die Zeichenkette mit der Maschine.
Der Symbol-Algorithmus
Zunächst wird die Liste Cn der zu verarbeitenden Zahlen aufgestellt (1..20). Bn ist die Positionsnummer. Wichtig ist die Liste CPn, die mit dem Zeichen L beginnt, das der 1 zugeordnet ist (Bn = 1). Die 1 hat eine Sonderrolle, ist weder prim noch zusammengesetzt. Interessant wird es ab Bn = 2. Zu Beginn wird 2 als prim eingestuft. Nun folgen die Teilprozesse:
- Das erste L wird verschoben und gehört nun zur Zahl 3.
- Das Wort L wird Bn = 2 mal notiert, das zweite an das Ende der bisherigen Kette anschließend. CPn = LL, zugeordnet den Zahlen 3 und 4.
- Von Bn = 2 aus zählt man in 2er-Schritten weiter: 3, 4. Das zeigt, dass 4 ein Vielfaches von 2 ist, daher wird das zweite L in ein M umgewandelt. Das ist äquivalent damit, die Vielfachen von Bn bis zum aktuellen Ende von CPn zu kontrollieren und ggf. ein L in ein M zu verändern. CPn = LM.
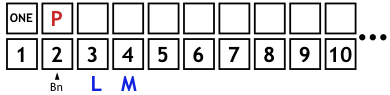
Bn = 3. Das L stuft 3 als prim ein. Nun folgen wieder die Teilprozesse:
- Das L kommt ans Ende der Kette und die Zuordnung von CPn beginnt jetzt bei der Zahl 4. CPn = ML.
- Die Kette ML wird Bn = 3 mal notiert, jeweils an das Ende der bisherigen Kette anschließend. CPn = MLMLML, zugeordnet den Zahlen 4 bis 9.
- Man bemerkt, dass 9 ein Vielfaches von 3 ist, daher wird das dritte L in ein M umgewandelt (im 3er Rhythmus abzählen). Vorher war die 9 ein Primzahlkandidat, aber die Prüfung hat das korrigiert. CPn = MLMLMM.
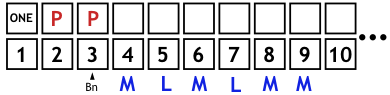
Bn = 4. Das M stuft 4 als zusammengesetzt ein. Erneut die Teilprozesse:
- Das L kommt ans Ende der Kette und die Zuordnung von CPn beginnt jetzt bei der Zahl 5. CPn = LMLMMM.
- Da 4 nicht prim ist, wird nichts kopiert.
- Jede Zahl mit der Zuordnung M ist sicher zusammengesetzt. Daher ist auch nichts zu ändern.
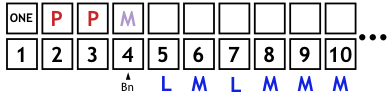
Bn = 5. Mit L zu Beginn ist die Zahl 5 als prim einzustufen. Noch einmal die Teilprozesse:
- Das L kommt ans Ende der Kette und die Zuordnung von CPn beginnt jetzt bei der Zahl 6. CPn = MLMMML.
- Die Kette ML wird Bn = 5 mal notiert, jeweils an das Ende der
bisherigen Kette anschließend.
CPn = MLMMML MLMMML MLMMML MLMMML MLMMML, zugeordnet den Zahlen 6 bis 35.
- Zwei der L in der Kette treffen Vielfache von 5 (25 und 35), daher sind zwei Umwandlungen vorzunehmen.
CPn = MLMMMLMLMMMLMLMMMLMMMMMLMLMMMM.
Der Algorithmus setzt sich auf diese Weise prinzipiell endlos fort, wir stoppen hier die Betrachtung.
Die bedeutsame Verlängerung der Kette CPn
Beim lezten Schritt haben wir auf die tabellarische Darstellung verzichtet.
Es fällt auf, dass sich durch die Vorschrift der Vervielfachung mit dem Faktor Bn bei ● copy
die Länge von CPn erst leicht und dann dramatisch erhöht. Es beginnt mit 1 und die Längenstufen
sind das Produkt der abgearbeiteten Primzahlen:
$$1, 2, 6, 30, 210, 2310, 30030, 510510, 9699690, ...\text{mit } 2\cdot 3\cdot 5\cdot 7\cdot 11\cdot 13\cdot 17\cdot 19=9699690.$$
Man kann den Algorithmus nur einführend von Hand präsentieren, danach muss eine Maschine eingesetzt werden. Aber auch die Maschine gelangt bei diesem Algorithmus schnell an ihre Grenzen: Speichergröße und Rechenzeit "explodieren" mit dem Faktor Bn. Würde man den Algorithmus um den Faktor 100 optimieren, führte dies bereits nach zwei weiteren Stufen erneut zum Kollaps.
Das Muster der Primzahlverteilung
Wie eingangs erwähnt, geht es nicht darum, neue Primzahlen schnell zu finden; die Erforschung zielt auf die Erkennung des Musters bei der Verteilung der Primzahlen und der Lücken (Gaps) in der Menge der natürlichen Zahlen.
Lesen Sie die komplette Dokumentation zum mathematischen Hintergrund.