Fractal Home
Heeren-Symbol-Algorithmus: Dust
Wer sich mit Fraktalen auskennt, hat wahrscheinlich schon einmal etwas von Cantorstaub
oder der Cantor-Menge gehört. Man beginnt mit dem Intervall $[0,1]$ der reellen Zahlen.
Das mittlere Drittel wird entfernt, sodass links und rechts die Intervalle $[0,\frac{1}{3}$
und $[\frac{2}{3},1]$ stehen bleiben. Mit diesen Intervallen führt man den Algorithmus sinngemäß fort.
Auf den ersten Blick ähnlich erscheint der Heeren Dust, allerdings wird die Darstellung
mit jeder Stufe skaliert. Der Algorithmus ist auch nicht einfach regelmäßig; er orientiert
sich an der Verteilung der Zeichen L und M in der Kette CPn und korreliert mit der
Verteilung der Primzahlen in den natürlichen Zahlen.
Einordnung und Vergleich
Die Cantormenge ist ein Fraktal mit einem regelmäßigen Algorithmus mit immer derselben Reduktion von zwei Dritteln pro Schritt. Der Heeren Dust wird ebenfalls von einem fixen Algorithmus gesteuert, aber die Reduktion ist viel größer, da die Lücken M in der wachsenden Zeichenkette CPn exponentiell größer werden. Wie bei jedem Fraktal gibt es Selbstähnlichkeit im Aufbau und in beiden Fällen auch eine gebrochene Dimension.
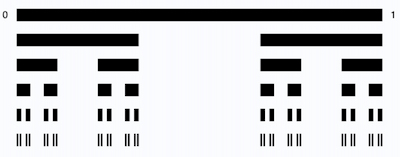
Heeren Dust: Die Kette CPn
Fraktaler Algorithmus basierend auf Symbolketten-Transformationen
mit Darstellung der Entwicklung des fraktalen Musters CPn. Dabei werden die Zeichen L
als Rechteck und die Zeichen M als Lücke dargestellt.
Die Breite der Rechtecke wird so angepasst, dass die Zeichenkette CPn den
Darstellungsbereich komplett ausfüllt. Wenn die Breite ein Pixel unterschreitet,
bricht das Programm ab.