Heeren Primes Symbol Algorithm Page 2

Heeren Symbol Algorithm: Dust

If you are familiar with fractals, you probably already heard about the Cantor Set or the Cantor Dust. It starts with the interval $[0,1]$ of the real numbers. The middle third is removed, so that in left and right the intervals $[0,\frac{1}{3}$ and $[\frac{2}{3},1]$ remain. With these intervals, the algorithm is continued like before.
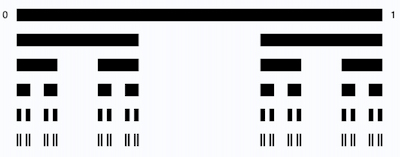
At a first glance, the Heeren Dust appears similar, but the representation is scaled with each level. The algorithm isn't simply regular, but belongs to the distribution of the characters L and M in the chain CPn and correlates with the distribution of prime numbers in the natural numbers.

The Cantor Set

A Comparative Overview

The Cantor set is a fractal with a regular algorithm which always has the same reduction factor of two thirds per step. The Heeren Dust is also produced by a fixed algorithm, but the reduction is much bigger because the gaps M in the evolving string CPn become exponentially larger. As with every fractal, there is self-similarity in the structure and in both cases a broken dimension.

Heeren Dust: The Chain CPn

Fractal algorithm based on symbol chain transformations showing the evolution of the fractal pattern CPn. The characters L are represented as a rectangle and the characters M as a gap.
The width of the rectangles is adjusted so that the character string CPn completely fills the display area. If the width is less than one pixel, the program aborts.