Fractal Home
Hyperbolic Ornaments
The Dutch artist M. C. Escher (1898-1972) has created many images, which are well known and respected until today. Especially the friends of mathematics love his pictures. Escher was inspired by his friend, the mathematician Harold S. M. Coxeter, and the result is a series of graphics titled Kreislimit I - IV. In mathematical view the images are Hyperbolic Ornaments.
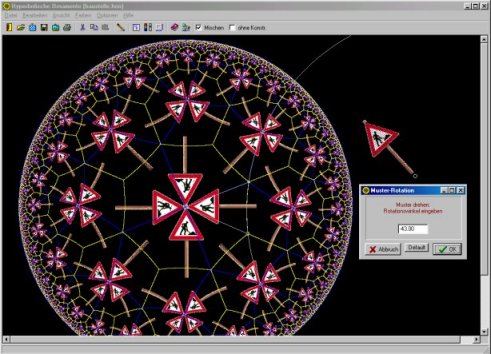
Program "Hyperbolische Ornamente"
Fractal Hyperbolic Ornaments
On principle the canvas is a unit-circle ideally tesselated with a non overlapping pattern.
The tesselation is constructed of mirror images of a basic element. The reflections at the three sides of a hyperbolic triangle are iterated, meaning that the results are reflected again and again. You can use the parts of the triangle as basic elements as well as imported pictures.
Because the third side of the triangle is part of a circle, those circle reflections are deformed. If all rules are respected, the sequence of reflections stays in the unit circle and the ornament is formed perfectly. If the basic element is a fractal image you may call the result Fractal Hyperbolic Ornament.
The program
My program "Hyperbolische Ornamente" was used to draw the images on this page. The program contains a help file (written in German!), that explains the mathematical background of Hyperbolic Ornaments and instructs about the use of the program. After editing a few parameters the basic image could be drawn. It is possible to import a small image of any origin and use it as a basic pattern. The location of the image and the boundaries of the ornament are influenced by mouse motions. The imported pattern could be rotated, the angle is infinitely variable. In exchange for your own product you can order the program for download.
To be continued
The next page is the interactive part of Hyperbolic Ornaments combined with a little bit of theory around the subject..




