Fractal Home
Heeren Symbol Algorithm for Prime numbers
Anyone with an interest in mathematics has heard of the Sieve of Eratosthenes for determining prime numbers. Many other methods are based on optimizations of this sieve. In higher mathematics, algebraic methods exist to speed up the search.
Why do not try a completely different approach? In 2007, Birke Heeren
developed a symbolic algorithm using paper strips and symbol cards in order
to construct a meaningful chain through regular manipulations of a few symbols. From this
chain, the positions of prime numbers and the gaps within the set of natural numbers emerge.
The motivation is not to compete with other methods, but more to explore this fractal
distribution pattern.
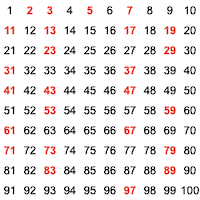
The Distribution of Prime Numbers
In his book The Music of the Primes, Marcus du Sautoy establishes the key questions:
Prime Number Distribution
"The primes are the atoms of arithmetic - numbers which can only be divided by one and themselves. At the same time, they are among the most tantalising and mysterious objects in mathematics. 2, 3, 5, 7, ... - can we predict what the next prime will be? Is there a pattern behind the rhythm of the primes?"
Researchers have been searching for answers to this questions for about 150 years. How are the prime numbers and the gaps between them distributed within the set of natural numbers?
Birke Heeren tried it herself and discovered an algorithm in which a few symbols are manipulated using three sub-processes:
● move ● copy ● change
These processes are applied in such a way that with each iteration step, information about the position of further gaps and prime numbers is revealed from the resulting character string CPn. Explore the steps and the character string using the machine.
The Symbol Algorithm
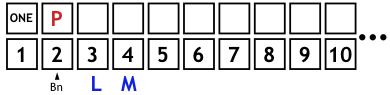
First, the list Cn of numbers to be processed is created (1..20). Bn is the position number. The most important list is CPn, which starts with the symbol L assigned to the number 1 (Bn = 1). The number 1 has a special role, being neither prime nor composite. Things get interesting from Bn = 2 onwards. Initially, 2 is classified as prime. Now the sub-processes follow:
- The first L is moved and now belongs to the number 3.
- The symbol L is noted Bn = 2 times, with the second one appended to the end of the existing chain. CPn = LL, assigned to the numbers 3 and 4.
- Starting with Bn = 2 you have to count in steps of 2: 3, 4. That means, 4 is a multiple of 2, therefor the second L changes to M. This is equivalent to checking the multiples of Bn up to the current end of CPn and, if necessary, changing an L to an M. CPn = LM.
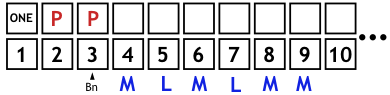
Bn = 3. The L classifies 3 as prime. Now the sub-processes follow again:
- The L is moved to the end of the chain, and the assignment of CPn now starts at the number 4. CPn = ML.
- The chain ML is written Bn = 3 times, always appended to the end of the existing chain. CPn = MLMLML, now is assigned to the numbers 4 through 9.
- Notice that 9 is a multiple of 3, so the third L is changed to an M. Previously, 9 was a prime number candidate, but the check has corrected this. CPn = MLMLMM.
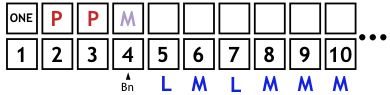
Bn = 4. The M classifies 4 as a composite number. Again, the sub-processes follow:
- The L is moved to the end of the chain, and the assignment of CPn now starts at the number 5. CPn = LMLMMM.
- Since 4 is not prime, nothing is copied.
- Any number assigned an M is definitely composite. Therefore, there is nothing to be changed.
Bn = 5. With L at the beginning, the number 5 is classified as prime. Once again, the sub-processes follow:
- The L is moved to the end of the chain, and the assignment of CPn now starts at the number 6.
CPn = MLMMML.
- The chain ML is written Bn = 5 times, always appended to the end of
the existing chain.
CPn = MLMMML MLMMML MLMMML MLMMML MLMMML, assigned to the numbers 6 through 35.
- Two of the L in the chain belong to multiples of 5 (25 and 35), two changes have to be made.
CPn = MLMMMLMLMMMLMLMMMLMMMMMLMLMMMM.
The algorithm is continued this way, theoretically ad infinitum. We will stop our explication here.
The Significant Elongation of the CPn Chain
In the last step, we omitted the tabular representation.
One observes that the rule of multiplication by the factor Bn during ● copy
causes the length of CPn to first increase slightly and then dramatically. It starts at 1,
and the successive lengths are the product of the processed prime numbers:
$$1, 2, 6, 30, 210, 2310, 30030, 510510, 9699690, ...\text{with } 2\cdot 3\cdot 5\cdot 7\cdot 11\cdot 13\cdot 17\cdot 19=9699690.$$
The algorithm can only be presented manually as an introduction; thereafter, a machine has to be used. But even a machine quickly reaches its limits with this algorithm: memory size and computation time "explode" by the factor Bn. If you could optimize the algorithm by a factor of 100, it would lead to a collapse again after just two more steps.
The Pattern of Prime Number Distribution
As mentioned at the beginning, the goal is not to find new prime numbers in fast mode. The research aims to recognize the pattern in the distribution of prime numbers and the gaps (Gaps) within the set of the natural numbers.
Read the complete documentation on the mathematical background.