Fractal Home
Der Quellcode ist hyperbolic.js. Danke an Eric Rowell für KineticJS. Der Quellcode dieser HTML-Seite zeigt die Einbindung. Mehr: Experimentelle Maschine mit Bildern...
Hyperbolische Maschine
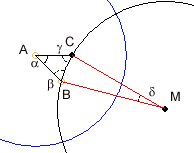
Grundkonstruktion ist ein hyperbolisches Dreiecks ABC mit den Winkeln α, β und γ, die durch die natürlichen Zahlen k, n und m als Bruchteile von 180° gegeben werden.
α = 180°/k, β = 180°/n und
γ = 180°/m mit der Bedingung
1/k + 1/m + 1/n < 1
Das Dreieck hat zwei gerade Seiten sowie eine mit Kreiskrümmung mit Mittelpunkt M. Der Mittelpunkt M (weiß) liegt außerhalb des Bildkreises. Man legt durch Verschieben des gelben und des orangenen Kringels die Punkte A, B fest. Die Restkonstruktion nimmt die Maschine vor. C ist durch die Winkel und durch AB bestimmt. Die Winkel β und γ werden jeweils zwischen den geraden Schenkeln und den Kreistangenten gemessen. Die Winkelsumme im hyperbolischen Dreieck ist kleiner als 180°.
Da die Radiuslinien senkrecht zum Kreisrand des Kreises um A (gelb) stehen müssen, ist mit dem Dreieck auch der Winkel δ und die Lage des Mittelpunktes M für den Konstruktionskreis bekannt. Der blaue Kreis schneidet den Konstruktionskreis orthogonal. Sind die Winkel des hyperbolischen Dreiecks durch die natürlichen Zahlen k, m, und n und die links notierten Bedingungen festgelegt, ergeben sich folgende interessante Konsequenzen:
- Die Bilddreiecke, die bei der iterativen Spiegelung des Ausgangsdreiecks an seinen Seiten entstehen, pflastern den blauen Kreis lückenlos und überschneidungsfrei.
- Die Bildpunkte der Ecken sind wie die Ausgangspunkte Drehpunkte derselben Ordnung.
Bedienung: Wählen Sie k, n, m nach den Bedingungen. Ist das Bild zu dünn, wiederholen Sie das Zeichnen oder erhöhen die Werte für Dots und Iterations. Sofern angehakt, führt die Maschine Spiegelungen an der Strecke AB, an der Strecke AC bzw. am Kreisbogen BC aus.
