Bildung
Die anderen Verteilungsdiagramme
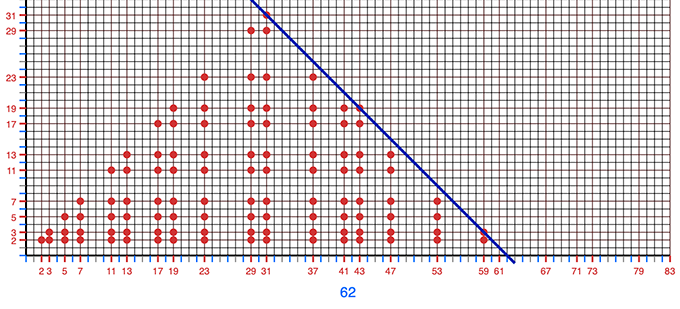
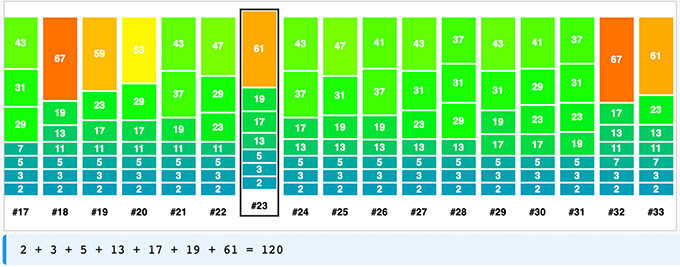
Das Diagramm für den Modus 2: $n=p+q$ weist eine interessante Komplexität auf. WEnn man unten die Maschinen startet, kann man sich die Diagramme zur Goldbachzahl der anderen Modi 3, 4 und 5 anschauen.
Wir sehen jeweils die Golbachzahlen (y-Achse) aufgetragen über der Zerlegungszahl $n$ (x-Achse).
Die 3er, 4er und 5er Verteilungsdiagramme
Die Darstellungsautomaten dazu öffnen sich als separate HTML-Seiten. Lassen Sie die Darstellungen berechnen und vergleichen Sie die Diagramme.
Beobachtungen, Erklärungen und ein Fazit
Aus der analytischen Zahlentheorie ist bekannt, dass das 2er-Diagramm ungefähr logarithmisch ansteigt. Je größer $n$ wird, desto mehr mögliche Paare $(p, n-p)$ gibt es, desto größer wird der Suchraum an Primzahlen; die Primzahlen werden jedoch seltener.
Die Primzahldichte um $x$ ist nämlich ungefähr $\displaystyle\frac{1}{\ln x}$.
Daher ist die Wahrscheinlichkeit, dass sowohl $p$ als auch $n-p$ Primzahlen sind, ungefähr
$$\omega = \displaystyle\frac{1}{\ln p} \cdot \frac{1}{\ln(n-p)} \approx \frac{1}{(\ln n)^2}.$$
Da es etwa n mögliche Werte für p gibt, erwartet man $G(n) \approx \displaystyle\frac{n}{(\ln n)^2}$.
Der Zähler steigt linear, aber der Nenner mit $(\ln n)^2$.
Das bedeutet: Wachstum, aber die Bremsung durch die fallende Primzahldichte dominiert
asymptotisch, daher der rechtsgekrümmte Graph.
Die komplexen Feinstrukturen im Diagramm sind das Ergebnis eines statistischen Trends, der durch modulare Strukturen und Resonanzen der Primzahlen in feine Bänder, Peaks und Täler zerlegt wird — chaotisch im Detail, geordnet im Großen. Die Verteilung der Primzahlen in der Menge der natürlichen Zahlen wird immer noch erforscht.
Man weiß, dass alle Primzahlen > 3 nur in den Restklassen 1 und 5 mod 6 liegen. Das erzeugt erkennbare Streifen im klassischen Goldbach-Diagramm.
Die Verteilungsdiagramme höherer Ordnung
Es fällt sofort auf, dass die Graphen für die Modi 3, 4 und 5 alle linksgekrümmt sind, also beschleunigt wachsend. Die analytische Zahlentheorie deutet das anhand der errechneten Anstiegsterme. Die sind im Einzelnen:
- Modus 3: $\displaystyle\frac{n^2}{(\ln n)^3}$
- Modus 4: $\displaystyle\frac{n^3}{(\ln n)^4}$
- Modus 5: $\displaystyle\frac{n^4}{(\ln n)^5}$
Demnach wachsen die Nenner, aber viel langsamer als die Zähler. Der Logarithmus kann die schnell wachsende Potenz nicht mehr bremsen, wie noch erkennbar im 2er-Diagramm. Generell gilt: Je mehr Summanden, desto stärker die Links-Krümmung
Eine weitere Beobachtung
Die Strukturen verschwinden mit der Erhöhung der Summandenzahl. Die für Modus 2 noch sichtbaren Muster nehmen nach und nach ab. Bei vielen Summanden gibt es für jede Summe viel mehr Kombinationen, so dass weniger Lücken entstehen. Die Verteilungen werden nach und nach glatter, der Mittelwert stabiler, rauschärmer.
Bei einer großen Summandenzahl (z.B. 7 Summanden) wirkt die Verteilung wie ein glattes Polynom ohne erkennbare Struktur.
Hier liest man die Zerlegungen der Zahl 62 an den Schnittpunkten der Geraden mit den roten Punkten ab.
Die Summandenanzahl lässt sich steigern: Die Zahl 120 als Summe von 7 Primzahlen