Philosophische Gedanken
Gefahr erkannt,
Gefahr gebannt.
SUVA Slogan
Über die Gültigkeit von Simulationen
Warum überhaupt Simulationen mag sich manch einer fragen. Welchen Nutzen bringt es, mehrere Stunden mühsamer Arbeit in ein Computerprogramm zu investieren, wenn man denselben Effekt in Natura beobachten kann? Wir haben uns dazu folgende Gedanken gemacht:
a) Gründe, die für eine Simulation sprechen:
- Senkung des Material / Kostenaufwands. Man denke zum Beispiel an Crash-Tests in der Fahrzeugentwicklung. Es ist weder gratis noch umweltfreundlich einen Prototypen eines Autos samt sensorbestückten Dummies zu Schrott zu fahren und dann auch noch zu entsorgen.
- Universeller Einsatz. Ist ein Simulationsprogramm erst einmal entwickelt worden, kann es schnell und beliebig oft modifiziert und ausgeführt werden. Man hat damit die Möglichkeit mit demselben Programm jedes beliebige Auto auf seine Unfallsicherheit zu testen. So oft man will.
- Senkung von Risikofaktoren. Ein Hochhaus kann beispielsweise mit der Simulation eines Erdbebens auf Konstruktionsmängel getestet werden, noch bevor überhaupt das Fundament gelegt wurde.
- Senkung des Zeitaufwands. Ein Ingenieur konstruiert eine Brücke. Anstatt umständliche Modelle zu bauen und diese zu testen, ist es oft schneller eine Computersimulation laufen zu lassen. Auf diese Weise ist auch die sonst zeitaufwendige Datenerfassung schon erledigt, die für die Konstruktionspläne erforderlich ist.
- Vereinfachte Analyse von Zusammenhängen durch rasches Ändern von Parametern. In ein Computerprogramm kann man jederzeit eingreifen und es beliebig verändern. Untersucht zum Beispiel ein Wissenschaftler die Relation zwischen Grundwasser und Waldbestand, so kann er auf dem Computer nach Gutdünken Bäume entfernen und ebenso schnell wieder hinsetzen.
- Finden von Optimallösungen. All die bisher genannten Punkte laufen schlussendlich auf ein und dasselbe hinaus: Durch Simulationen können Optimallösungen für beinahe jedes Problem zu erschwinglichen Kosten gefunden werden.
b) Gründe, warum man mit einer Simulation vorsichtig umgehen sollte:
- Mathematische Fehler können unbemerkt bleiben. Wenn irgendwo im Programm ein Fehler herumgeistert, so muss der Programmierer das nicht unbedingt bemerken. Ein Restrisiko bleibt immer, was zum Beispiel bei Gebäudekonstruktionen fatale Auswirkungen haben könnte.
- Restfehler bleiben immer. Da ein Computer nur mit endlicher - wenn auch sehr hoher - Genauigkeit rechnen kann, entstehen immer Rundungsfehler. Auch diese sind beim Simulationsergebnis zu berücksichtigen.
- Beschränkte Anzahl von Faktoren. Um eine Problemstellung für die Maschine berechenbar zu machen, muss sie abstrahiert werden. Man muss das Problem aus seinem Umfeld herausnehmen. Dabei fallen Einflussquellen weg. Zwar nur kleine, aber deren viele.
- Konstruktionsfehler. Es können auch unbemerkt wichtige Einflussquellen vergessen oder falsch mit dem Problem in Zusammenhang gebracht werden.
- Interpretationsfehler. Auch wenn die ganze Simulation stimmt, so kann sie falsch oder fehlerhaft ausgewertet werden.
Wir sollten uns dessen stets bewusst sein, wenn wir mit dem Wundermittel Simulation arbeiten. Das genaue Abschätzen der Verhältnisse zwischen Investition, Gewinn, Verlust- und Fehlerrisiko empfiehlt sich in jedem Fall.
Wir untersuchen nun in groben Zügen den Aufbau einer Simulation. Das Schema gibt auf einfachste Weise den Programmablauf wieder.
Als Eingabe kann alles mögliche dienen: Zahlen (Parameter), Buchstabenfolgen,
Bilder, etc. Täglich werden in meteorologischen Zentren Simulationen
durchgerechnet, die die aktuelle Wetterlage als Eingabe haben. Auch die
Ausgabe des einen Programms kann als Eingabe für das andere dienen.
Alle Eingaben müssen aber vom Computer in Zahlen umgeformt werden,
damit er überhaupt etwas damit anstellen kann.
Ebenso die Form der Ausgabe können wir beliebig wählen. Zahlen,
Bilder, Bildfolgen, einfach alles, das auf dem Bildschirm oder dem Drucker
realisierbar ist.
Der interessanteste Teil ist die Operation. Wie gelangt der Computer
von der Eingabe zur Ausgabe?
Prinzipiell basiert jedes Computerprogramm auf einem Algorithmus:
Definition eines Algorithmus:
Ein Algorithmus ist eine Folge von eindeutig bestimmten Anweisungen, mit deren Hilfe aus gegebenen Anfangswerten ein Ergebnis berechnet werden kann.
1Aus Grundkenntnisse EDV S.13
Das Wort Algorithmus stammt vom persischen Mathematiker Alchwarismi, der um 900 in Bagdad wirkte.
Grundsätzlich bestehen diese eindeutig bestimmten Anweisungen nur aus mathematischen Operationen. Wie wir aber bereits im Kapitel "Hinweise zu den Algorithmen" gezeigt haben, können Anweisungsfolgen in Routinen zusammengefasst werden. Auf jedem PC sind schon Tausende dieser Routinen gespeichert, so dass wir uns nicht mehr mit Basisoperationen herumschlagen müssen. Es stehen uns neben allen mathematischen Funktionen Operationen zur Verfügung, mit denen wir
- Graphische Elemente (Linien, Punkte, Rechtecke, ... in Farbe)
- Textelemente (Buchstabenoperationen, Schriften etc.)
- Datenspeicherung und Abruf
- Eingabehilfen (Textfelder, Buttons, ...)
- Layout und Benutzeroberflächen
mit wenigen Befehlen realisieren können.
Die Schwierigkeit besteht nun darin, den richtigen Algorithmus zur
Lösung eines Problems zu finden. Wir kennen dazu zwei Strategien:
a) Experimenteller Weg
- Festlegen einer Theorie über das Verhalten des realen Objekts
- Nichtformales Aufstellen eines Algorithmus nach der Theorie
- Vergleichen des Ergebnisses mit der Natur
- Korrekturen an der Theorie und / oder am Algorithmus vornehmen
- Erneutes Testen und korrigieren bis die gewünschten Ergebnisse vorliegen.
b) Rechnerischer Weg
- Physikalische Eigenschaften des realen Objekts ermitteln
Formales Aufstellen eines Algorithmus nach den physikalischen Gegebenheiten
Vergleichen des Ergebnisses mit der Natur
Korrekturen am Algorithmus vornehmen
Erneutes Testen und korrigieren bis die gewünschten Ergebnisse vorliegen.
Für unsere Themen, die eng in Verbindung zur lebendigen Natur stehen,
eignet sich der experimentelle Weg wesentlich besser, da das Sammeln von
physikalischen Daten auf diesem Gebiet sehr zeitraubend wäre. Der
experimentelle Weg ist weniger aufwendig und liefert im Allgemeinen recht
brauchbare Ergebnisse.
Dieser Weg birgt jedoch ein großes Fehlerrisiko in sich: Die
Ausgabe kann sogar sehr genau mit der Wirklichkeit übereinstimmen,
aber der Konstruktionsweg ein trotzdem gänzlich falscher sein.
Uns darf nicht nur das bloße Endergebnis der Simulation interessieren,
sondern insbesondere haben wir die Zeit, das heißt den Konstruktionsablauf
zu berücksichtigen.
Das folgende Bild zeigt zwei Konstruktionsabläufe, die beide das gleiche Resultat zur Folge haben.
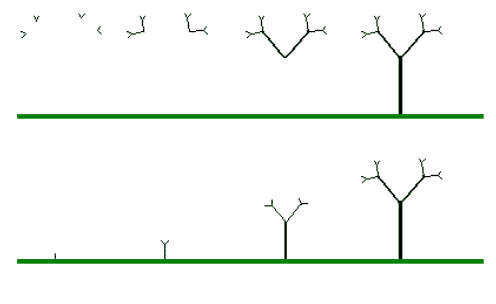
Bild N° 1: Konstruktionstopologie
Um einen Baum zu konstruieren, ist schematisch nur
die untere Methode "topologisch" richtig. Die obere könnte man zum
Beispiel benutzen, um einen Flusslauf auf einer schiefen Ebene darzustellen.
(Dass beide Konstruktionen, die eines Baumes und die eines Flusslaufes
ein ähnliches Endergebnis haben, ist nicht weiter verwunderlich: Beide
folgen dem gleichen Ideal mit möglichst wenig Gesamtstrecke ein möglichst
großes Einzugsgebiet zu erreichen.2
Man beachte, dass es sich hierbei nur um ein Schema handelt, an dem
wir den Begriff "Konstruktionstopologie" zu erläutern versuchen.
Genaue Modelle werden wir später erstellen.
Ein frappierendes Beispiel hierzu ist die (falsche) Konstruktion eines sehr echt wirkenden Farnblattes durch ein iteriertes Funktionssystem (IFS). Jeder Iterationsschritt der Konstruktion besteht darin, von einem Punkt(x(0), y(0)) auf dem Koordinatensystem mit Hilfe von mehreren Funktionen einen weiteren Punkt(x(1), y(1)) zu berechnen. Vom Punkt (x(1), y(1)) dann den Punkt (x(2), y(2)) und so weiter bis zum Punkt (x(n), y(n)).3
2Mehr zu diesem Thema in Peter Stevens "Formen der Natur". [zurück]
3Michael Barnsley untersucht in seinem Buch "Fractals everywhere" iterierte Funktionssysteme genauer.


Bild N° 2a) IFS Farn, Bild N° 2b) Echter Farn
Diese Konstruktionsweise zeigt in keiner Weise Ähnlichkeit mit
dem Wachstumsprozess eines Farns und ist damit für Simulationen völlig
ungeeignet.
Die Konstruktionstopologie ist wohl die wichtigste Komponente jeder
computergestützten Simulation. Trotzdem wird sie in mehreren uns bekannten
Fällen völlig außer Acht gelassen. Dies gilt insbesondere
für oft unwissenschaftliche Internetpublikationen. Eine Überprüfung
ist selbst in der Fachliteratur dringend nötig.