L-Systeme - Pflanzen
Visualisierung
Die folgende Liste von Arbeitsschritten1 hilft bei der Planung der Arbeit:
- Wir analysieren das Objekt in mehreren Zuständen in der Natur (Beobachtung) und / oder in einem Laboratorium
- Wir stellen auf nichtformalem Weg die Regeln auf
- Wir bringen die Regeln und den Anfangszustand durch ein L-System zum Ausdruck
- Wir lassen eine Simulation auf dem Computer laufen, die eine lange Zeichenkette erzeugt.
- Wir übersetzen das Resultat in eine graphische Ausgabe
- Wir vergleichen das Bild (oder mehrere Bilder von verschiedenen Stadien) mit dem Verhalten des wirklichen Objekts
- Wir nehmen falls nötig Korrekturen vor und wiederholen die erforderlichen Schritte.
1Aus H.O.Peitgen: "Chaos, Bausteine der Ordnung", S. 514
Mit Hilfe der Erkenntnisse der Blattstellungslehre ist es einfach, das zweidimensionale L-System in ein konstruktionstopologisch richtiges 3D-L-System umzuwandeln. Nennen wir den Divergenzwinkel ρ und den Achsenwinkel α. Dann heißen ab jetzt die Schildkrötenbefehle:
+ Drehe dich um die eigene Achse im Winkel ρ
- Drehe dich um die eigene Achse im Winkel -ρ
/ Neige dich im Winkel α
\ Neige dich im Winkel -α
Die Drehungsachse des Divergenzwinkels definiert sich durch die Schnittmenge der Frontalebene und der Saggitalebene (y-Achse), die des Neigungswinkels durch die Schnittmenge der Saggitalebene und der Horizontalebene (z-Achse). Das Koordinatensystem bewegt sich stets mit der Schildkröte (d.h. die y-Achse verläuft stets vom Kopf zum Schwanz, die z-Achse vom Bauch zur Panzerdecke).
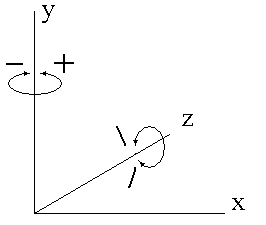
Bild N° 1: Rotationsachsen
Zur graphischen Interpretation verwenden wir einfache geometrische Körper
wie Kugeln, Zylinder, Würfel etc.
Das Wort F[/B]F-[/B]F-[/B]FK würde für α = 45° und ρ = 180° folgendermaßen
aussehen:
(F = Zylinder, B = skalierter Würfel, K = Kugel):
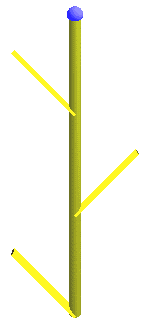
Bild N° 2: 3D-Interpretation
Die besprochenen Blattstellungstypen lassen sich sehr einfach durch ein L-System darstellen. Die Grundkonstruktionen sind...
...für die dekussierte Blattstellung:
F → E[/F][\F]+F für ρ = 90°
...für die spiralige Blattstellung
F → E[/F]+F für ρ = 180°, 120°, 144°, 135°, ...
...für die quirlige Blattstellung
F → E([/F]+)n +F, wobei n die Anzahl der Verzweigungen angibt.
Wie wir im vorangehenden Kapitel erwähnt haben, arbeiten gewisse Pflanzen mit Signalstoffen, d.h. ein Stoff "wandert" von einem Punkt in der Pflanze zu einem anderen. Das können wir mit Kontext freien L-Systemen nicht simulieren. Wir beschreiben an dieser Stelle kurz die Notationsweise von kontextsensitiven L-Systemen (Beispiele):
S < F → E Ein F wird zu einem E, wenn es vor einem S steht.
F > S → E Ein F wird zu einem E, wenn es hinter einem S steht.
T < F > S → E Ein F wird zu einem E, wenn es vor einem T und hinter einem S steht.
Ein Signal S kann in einer Zeichenkette also wie folgt weitergegeben werden:
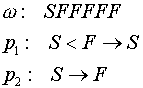
Das L-System erzeugt die Zeichenketten SFFFFF, FSFFFF, FFSFFF, FFFSFF, FFFSFF, FFFFSF. Das Signal wandert also wie gewünscht von der einen zur anderen Seite.