Chaotische Symmetrien [Exkurs 1]
Um die Rechenfähigkeit des Computers an dieser Stelle zu demonstrieren, wählen wir eine recht einfache Methode um spektakuläre und äußerst formschöne Bilder zu berechnen. Durch eine bestimmte Formel, die wir auf eine komplexe Zahl1 z0 anwenden erhalten wir eine neue komplexe Zahl z1. Mit derselben Formel berechnen wir aus z1 den Wert z2, aus z2 dann z3 und so weiter bis zu zt. Den ganzen Vorgang nennt man Iteration (lat. itero = wiederholen).
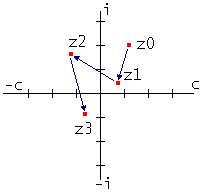
Bild N° 1: Iteration
Definition
1Eine komplexe Zahl besteht aus zwei Teilen.
Einem Realteil c, der eine beliebige reelle Zahl sein kann und einem Imaginärteil
i, wobei i als √-1 definiert ist. Beispiele:
z = (12 + 21i) oder z = ( -5.3 + 3.14i) oder z = (√2 – 0.9i). Komplexe Zahlen lassen sich auf einem Koordinatensystem mit der x-Achse c und der y-Achse i darstellen.
Eine gut verständliche Einführung in die komplexen
Zahlen findet sich in H.O. Peitgens Buch "Chaos – Bausteine der Ordnung"
Kapitel 4.2. [zurück]
Michael Field und Martin Globubitsky beschrieben in ihrem wunderschönen Buch "Chaotische Symmetrien" mehrere dieser Formeln. Wir wählen daraus
![F(z)=[l+azz'+b Re(z^n) + w i]z + cz^(-1-n) F(z)=[l+azz'+b Re(z^n) + w i]z + cz^(-1-n)](lsyspics/hzualg_f1.gif)
wobei λ, α, β, γ und ω reelle Parameter sind und n ein ganzzahliger Wert ist. Wir nehmen folgende Werte an:
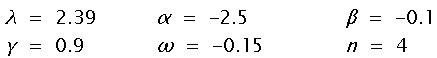
Die Werte für z bewegen sich innerhalb des Einheitskreises. Jeder
Punkt auf dem Koordinatensystem, der einmal getroffen wurde, wird gekennzeichnet.
Wenn man diesen Vorgang sehr oft wiederholt, entsteht aus diesen Punkten
ein symmetrisches Bild. Da weder Mensch noch Computer mit unendlicher Genauigkeit
rechnen können, müssen wir uns auf etwa 12 signifikante Dezimalstellen
beschränken. Zur Darstellung beschränken wir uns auf 4 Stellen
Genauigkeit. So können Punkte auch mehrmals getroffen werden, da ihre
Anzahl endlich ist.
Wir veranstalten nun ein Rennen zwischen einem Computer und einem Mathematiker.
Der Mathematiker ist mit Bleistift, Papier und einem Taschenrechner mit
12 Ziffern ausgerüstet, der die Funktionen +, -, *, /, sowie Wurzeln
und Potenzen beliebigen Grades berechnen kann. Der Computer ist mit einem
Programmierer und einem 166 MHz Prozessor ausgestattet. Gewonnen hat, wer
als erster ein gut erkennbares Bild errechnet hat.
Nach 65 Sekunden präsentiert der Computer das Ergebnis in Farbe
auf dem Bildschirm:

Bild N° 2: Chaotische Symmetrie
29004556 Punkte hat er berechnet und graphisch dargestellt (Die Farbe entspricht der Anzahl Treffer pro Punkt). Um dasselbe Resultat zu erreichen, müsste ein geübter Mathematiker noch schätzungsweise 552 Jahre lang pausenlos rechnen.
Man sollte sich stets dessen bewusst sein, dass mit dem leicht transportablen Personalcomputer jedermann ein Mittel gegeben ist, mit dem er einen Rechenaufwand betreiben kann, der noch vor fünfzig Jahren undenkbar gewesen wäre. 1970 leisteten "Supercomputer", die einige Tonnen schwer waren, ganze Hallen in Anspruch nahmen, über 10000000 Dollar kosteten und mehrere Mann Besatzung benötigten, nicht einen Hundertstel der handlichen PCs von 1999. Von einem Bildschirm ganz zu schweigen; die ersten Schwarzweißbildschirme kamen um 1975 in Umlauf (Sie mussten wegen ihres Gewichts von zwei Personen getragen werden). Personalcomputer gibt es erst seit etwa 1980.
Trotz ihrer ungeheuerlichen Geschwindigkeit sind Computer ungeheuerlich
dumm! Prompt führen sie jeden Befehl Null Komma Nichts aus, aber bei
der kleinsten Unstimmigkeit ist's aus und vorbei mit der Rechnerei. Zu
vernünftigem Handeln sind sie nicht fähig. Ebensowenig zur Einschätzung
und zum Verständnis von Problemsituationen. Befehle werden ausgeführt,
nicht verstanden.
Um einem Computer klare, eindeutige Befehle mitzuteilen, wurden im
Laufe der Zeit verschiedene Computersprachen entwickelt. Eine Folge von
Befehlen einer beliebigen Sprache nennt man Algorithmus (Eine genauere
Definition später). Wir werden vor allem mit zwei dieser Sprachen
arbeiten, nämlich mit BASIC und mit C++. Das Grundprogramm steht immer
in BASIC da, leicht verständlich und unkompliziert. Öfters müssen
wir aber besonders rechenintensive Programmteile in der etwas pingeligeren
Sprache C++ schreiben, weil sie so aus bestimmten Gründen wesentlich
schneller ausgeführt werden.
Die hier wiedergegebenen Programmteile sind alle durch ihre Schriftart gekennzeichnet. Für die Farbgebung gelten folgende Regeln:
- Kommentare werden grün markiert: 'Dies ist ein Kommentar in BASIC
Sie werden vom Programm nicht ausgeführt und dienen nur zur Orientierung für den Programmierer. Ein Kommentar wird mit dem Symbol ' (nur in BASIC) markiert. Die Einleitung eines Kommentars mit ' gilt für jede neue Zeile. Davon wird hier in der HTML-Darstellung abgewichen, weil der Zeilenumbruch nach Bildschirmgröße erfolgt. - Schlüsselwörter sind blau: End Sub
Schlüsselwörter sind reservierte Wörter, die alle ihre bestimmte und eindeutige Funktion haben. Ein Variablenname, ein Konstantenname oder der Name einer Routine dürfen niemals denselben Namen wie ein Schlüsselwort haben. Sonst entsteht ein hässlicher ... - Fehler (rot) End = 12
Hier wurde dem Schlüsselwort End ein Wert zugewiesen. - Der Rest ist schwarz. c = ( a * a + b * b ) ^ 0.5
Unmöglich können hier alle Möglichkeiten und Methoden,
alle Techniken der Programmierung aufgeführt werden. Wir haben alle
Programme möglichst ausführlich kommentiert und erklären
spezielle Winkelzüge anhand der konkreten Beispiele.
Trotzdem können wir nicht darauf verzichten, zwei grundlegende
Elemente der Programmierung in der Computersprache BASIC kurz zu streifen:
Die Variablen und die Routinen.
Variablen sind da, um Werte (Zahlen oder Buchstabenfolgen) zu speichern.
Man kann mit ihnen rechnen, aber sie werden keinesfalls in Sinne einer
algebraischen Unbekannten gebraucht. Jede Variable hat immer ihren eindeutigen
Wert. Der Name einer Variable kann ein oder mehrere Zeichen lang sein.
Ein Wert wird einer Variable mit einem = Zeichen zugeordnet:
i = 2 'Der Variable i wird der Wert 2 zugeordnet.
Pi = 3.1415 'Der Variable Pi wird der Wert 3.1415 zugeordnet.
MeinText = "Hallo" 'Der Variable MeinText wird die Buchstabenfolge "Hallo" zugeordnet.
Eine Rechnung kann also wie folgt geschrieben werden:
c = 12 * 34 'Der Variable c wird der Wert 12 * 34 zugeordnet. Der wert von c also ist 408.
k = i + Pi 'Der Variable k wird der Wert i + Pi also 2 + 3.1415 zugeordnet. k hat folglich den Wert 5.1415.
i = i + 1 'Der Variable i wird der Wert i + 1 also 2 + 1 zugeordnet. i hat jetzt den Wert 3.
Der Computer berechnet immer zuerst den Wert auf der rechten Seite des
Gleichzeichens und speichert dann die Antwort in der Variablen, die auf
der linken steht. Das letztere Beispiel, das in der Algebra einen totalen
Widerspruch bedeuten würde, heißt hier nichts anderes als "Zähle
zum Wert der Variable i eins dazu!"
Die Werte der Variablen werden nicht rückwirkend verändert.
Jede Zeile ist eine Anweisung für sich. In den zwei letzten Anweisungen
behält also k den Wert 5.1415 und wird nicht in 6.1415 geändert,
weil der Wert von i von 2 zu 3 geändert worden ist.
Die folgende Gleichung, die arithmetisch einfach zu lösen ist,
ist für den Computer völlig unverständlich:
i + 2 = 10 'Syntaxfehler
i + 2 ist keine Variable, und so weiß der Computer nicht, wo er
den Wert 10 auf der rechten Seite des Gleichzeichens speichern soll. Richtig wäre:
i = 10 – 2 'OK, Der Wert von i ist 8.
Es gelten folgende Arithmetische Zeichen: +,
-, *, /, ^, (,
). Das ^ steht für Potenzen.
c = ( a * a + b * b ) ^ 0.5 'Pythagoras-Satz. Anstelle der Wurzel wird mit 0.5 potenziert.
Ferner existieren noch eine Reihe von Spezialoperationen, die im Vocabular
näher beschrieben sind:
(Sin( ), Cos( ), Int( ), Abs( ), Sqr( ), Rnd( )...)
Man unterscheidet mehrere Typen von Variablen. Je nachdem wie große
Werte sie beinhalten sollen, muss man mehr oder weniger Speicherplatz für
sie reservieren. Die verschiedenen Variablentypen sind unter "Kleines BASIC-Vocabular"
aufgeführt. (Byte, Integer, Long, Single, Double, String).
Am Anfang jedes Programms definieren wir die Variablen und die Menge
Speicherplatz, die ihnen zur Verfügung stehen soll (Siehe Dim-Anweisung).
Ist ein Wert zu groß für eine Variable oder nicht konform, so
entsteht ein Fehler:
Dim i As Integer 'Definiere Variable i als "Integer" (= Ganzzahl zwischen -32768 und 32767, das entspricht
zwei Speichereinheiten)
i = 1000000 'Fehler: Überlauf
i = "Hallo" 'Fehler: Falscher Variablentypus. Buchstabenfolge anstatt einer Zahl
Sehr nützlich ist die Möglichkeit, auch ganze Variablenfelder
definieren zu können. Mit dem Befehl
Dim Kette(1 To 100) As Integer
haben wir hundert Variablen definiert, von Kette(1), Kette(2)... bis Kette(100). Auf die gleiche Weise können wir auch ein zweidimensionales Variablenfeld definieren:
Dim Feld(1 To 100, 1 To 100) As Integer
Routinen sind schnell erklärt. Unter einer Routine verstehen wir
eine separate Folge von Anweisungen, der wir einen Namen geben. Anstatt
die Anweisungsfolge können wir in unserem Hauptprogramm dann einfach
den Namen der Routine hinschreiben. Das ist insbesondere sinnvoll, wenn
diese Routine an mehreren Stellen des Programms vorkommt oder aus Gründen
der Übersichtlichkeit.
Eine Routine beginnt mit der Anweisung Sub und endet mit der Anweisung End Sub.
Beispiel:
Sub MeineRoutine() 'Hier beginnt die Routine mit dem Namen"MeineRoutine"
MeinText = "Halli Hallo"
i = i + 1
... 'Eine Folge beliebiger Anweisungen
End Sub 'Hier endet die Routine
Wenn ich also möchte, dass der Wert der Variable MeinText in die Buchstabenfolge "Halli Hallo" geändert wird und zur Variable i eins dazugezählt wird, so brauche ich ab jetzt nur noch MeineRoutine ins Hauptprogramm zu schreiben.
Oft werden wir zum besseren Verständnis Programmabläufe in Form von Algorithmenschemen oder Flussdiagrammen darstellen. Wir benutzen dafür die allgemeingültigen Symbole.2
2 Aus Grundkenntnisse EDV S.21
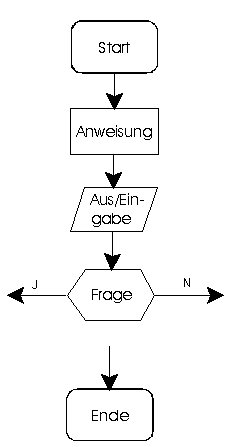
Bild N° 3: Flussdiagrammsymbole