Zelluläre Automaten - Bakterien
Geschichte und Funktionsweise der Zellulären Automaten
Die Idee eines zellulären Automaten ist so alt wie der Digital-
oder Elektronenrechner selbst.
Erste Versuche im Blickfeld des zellulären Automaten starteten
John von Neumann und Stanislaw Ulam Ende der 50er Jahre. Sie wollten ein
Computersystem entwickeln, das sich wie ein Lebewesen selbst reproduzieren
konnte. Erste greifbare Resultate mit demselben biologischen Hintergrund
fand 1968 John Horton Conway mit seinem "Spiel des Lebens" (LIFE). Bei
diesem "Spiel" werden Zellen geboren, überleben oder sterben je nach
der Anzahl ihrer Nachbarn.
Dass dieses Spiel später immense Wellen in der wissenschaftlichen
Forschung werfen würde, konnte Conway damals nicht ahnen.
LIFE ist sogar fähig einen Computer zu simulieren, zwar noch vereinfacht,
aber die entscheidenden Komponenten sind vorhanden (Schaltkreise).
Durch die große Bedeutung dieses Automaten haben wir beschlossen
ihn an dieser Stelle als erstes Beispiel aufzuführen.
Exkurs N° 8: LIFE
Stephen Wolfram, ein Kartograph in der Welt der
zellulären Automaten, widmete sich Ende 1982 vollständig der
Untersuchung von eindimensionalen zellulären Automaten.
Er beschränkte sich dabei auf "legale, totalistische Regeln".
Hierzu später mehr.
Nach Wolfram, der mit seinen Regeln möglichst komplizierte, vielseitige
Strukturen und Muster bilden wollte, kam der Drang nach einer gültigen
Simulation von Naturprozessen auf.
Es ging darum, die Natur mit möglichst einfachen Regeln nachzuahmen.
Das Wichtige dabei war, dass der Weg dem Naturvorgang entsprach, so dass
der Automat nicht nur ein ähnliches Endprodukt produzierte, sondern
dass man anhand des Automaten Rückschlüsse auf die Entstehung
der Struktur ziehen konnte (Siehe Kapitel "Über
die Gültigkeit von Simulationen"). Der zelluläre Automat hat
dadurch an Interesse gewonnen. Man kann ihn z.B. einsetzen um chemische,
biologische, sozialpsychologische, physikalische etc. Vorgänge zu
beschreiben.
Um die Funktionsweise eines zellulären Automaten zu erklären, muss man sich zuerst im Klaren sein, was das überhaupt ist. Wir erklären den Automaten als ein sich selbstreproduzierendes, aus vielen gleichartigen Zellen bestehendes auf Raum beschränktes mathematisches Gebilde.
Damit das Kriterium zellulärer Automat erfüllt ist, müssen verschiedene Grundbedingungen vorhanden sein.1
- Seine Entwicklung findet in Raum und Zeit statt.
- Sein Raum ist eine diskrete Menge zahlreicher Zellen.
- Jede dieser Zellen hat nur eine endliche Anzahl möglicher Zustände.
- Die Zustände der Zellen verändern sich in diskreten Zeitschritten.
- Alle Zellen sind identisch und verhalten sich nach den gleichen Entwicklungsregeln.
- Die Entwicklung der Zelle hängt nur ab von ihrem Zustand und dem ihrer sie lokal umgebenden Nachbarzellen.
1Definition aus Martin Gerhardt, Heike Schuster: "Das digitale Universum", S.18 [zurück]
Da es mit dieser theoretischen Skizzierung eines zellulären Wachstumsgebildes nicht getan ist, werden wir nachfolgend die einzelnen Komponenten einzeln erklären und mit einem praktischen Beispiel nachvollziehbar machen.
Der Lebensraum eines zellulären Automaten ist ein Gitter, dessen
Felder ausschließlich Informationen aus ihrer unmittelbaren Nachbarschaft
in die eigene Lebensentwicklung einbeziehen. Diese Felder werden Zellen
genannt, da sie den biologischen Bausteinen des Lebens entsprechen. Dieses
Gitter sollte möglichst fein gegliedert sein.
Ein sehr beliebtes Beispiel um dieses Spielfeld zu erklären, ist
das Billardspiel. Stellen wir uns einen Billardtisch vor, der eine Rasterung
aufweist (wie ein Schachbrett). Um die Bahn der Kugeln zu beschreiben,
ist eine Rasterung nötig, die Felder hat, die kleiner sind als die
Kugeln selbst. Sonst ist die genaue Position der Kugeln auf dem Tisch nicht
feststellbar. Um also eine sinnvolle Simulation zu erschaffen, muss auf
eine möglichst genaue Wiedergabe des Zellraums geachtet werden. Es
wäre auch möglich den Billardtisch mit nur zwei großen
Feldern zu simulieren, da diese Felder aber größer sind als
die Kugeln selbst, kann man keine genaue Position der Kugel festlegen.
Durch diese verschwommene Darstellung der Realität ist es äußerst
schwierig die Simulation sinnvoll auszuwerten.
Je nach Form und Dimension des realen Objekts gibt es eindimensionale
(die Zellen sind wie auf einer Perlenschnur aufgereiht), zweidimensionale
(das Spielfeld ist vergleichbar mit einem Schachbrett) und dreidimensionale
(z.B. Würfel) Lebensräume. Wichtig sind außerdem die Größe
der einzelnen Felder, deren Geometrie und die Gesamtgröße des
Spielfelds. Mögliche Gitterstrukturen wären zum Beispiel eine
sechseckige Wabenstruktur, fünfeckige Kreuzkonstruktionen oder schlicht
und einfach rechteckige Zellstrukturen. Wir beschäftigen uns ausschließlich
mit der quadratischen Aufteilung des Raumes, da diese Geometrie dem Computer
am besten entspricht.(vgl. Bild N° 3)
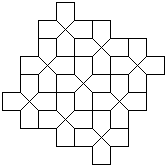
Bild N° 3: Fünfeckige Gittergeometrie
Wenn wir die Form der einzelnen Zellen festlegen, steuern wir auch auf eine bestimmte Anzahl von Nachbarn an. Eine sechseckige Form lässt beispielsweise auf 6 Nachbarn schließen. Bei den viereckigen Gitterstrukturen ergibt sich das Problem der diagonalen Nachbarn. Diesem geht man mit einer einfachen Definition aus dem Weg. Der Mathematiker von Neumann verwendete für seine Berechnungen nur die Zellen, die direkt an der Seite angrenzend waren, also keine diagonalen Nachbarn.
Sein Nachdenker Moore verwendete in seinen Berechnungen zusätzlich
die diagonalen Nachbarn. Es gibt also eine von Neumann und eine Moore
Nachbarschaft.
Diese Nachbarschaften kann man auch um zusätzliche Zellen erweitern.
Diese bilden einen weiteren Zellring um die anderen Nachbarn (siehe Bild N° 4).
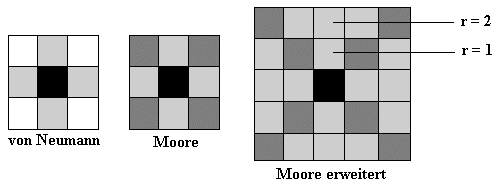
Bild N° 4: Nachbarschaften
Die Variable für den Radius der Nachbarschaft ist r. in einem eindimensionalen
Automaten beträgt die gesamte Nachbarschaft einer Zelle also 2r + 1.
Zur Definition des Lebensraumes gehört auch die Festlegung der Randbedingungen.
So kann, gleich einem alten menschlichen Weltbild, eine Zelle, die
den Rand des Spielfelds verläßt, sterben oder mit anderen Randbedingungen
z.B. auf der anderen Seite des Gitters wieder auftauchen.
Die Definition des Randes ist sehr wichtig, da die Randzellen weniger
Nachbarn haben als die Zellen in der Mitte. Dies kann mit Regeln, die nur
auf die Anzahl Nachbarn achten, zum raschen Aussterben der Randzellen führen.
Das dies sehr verhängnisvoll ist, zeigt die Tatsache, dass in einem
10 x 10 Felder umfassenden Gitter ca. 40 % aller Zellen Randzellen sind.
Die Mathematiker gehen diesem Problem aus dem Weg, indem sie beim eindimensionalen
Automaten einfach einen Ring bilden, beim zweidimensionalen einen Torus
und beim dreidimensionalen einen Hypertorus. Man spricht hier von periodischen
Randbedingungen.
Eine andere Möglichkeit dieses Problem zu lösen, ist die
Spieglung der Ränder. Diese Verknüpfung der Ränder nennt
man symmetrisch.
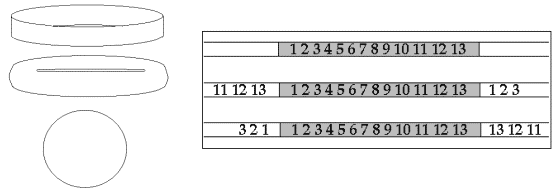
Bild N° 5: Randbedingungen
Dies waren die Komponenten, die wir für den Lebensraum der Automaten
antrafen.
Eine Kluft mit Kristallen weist z.B. die gleichen Merkmale auf:
- Die Größe des Raumes ist beschränkt
- Die Gitterstruktur entspricht der Molekülform der kristallbildenden Substanz.
- Es herrscht eine von Neumann Nachbarschaft mit Radius r = 1 vor.
- Die Randbedingungen sind dadurch überflüssig, da Zellen mit weniger Nachbarn nicht absterben, sondern erhalten bleiben.
Die Zellen definieren sich hauptsächlich durch ihre möglichen
Zustände. In einem binären Automaten kennen die Zellen nur zwei
verschiedene Zustände. Entweder tot oder lebendig. Beim Automaten
kann es aber auch Zwischenschritte geben, die z.B. das Altern simulieren
können. Bei Lebewesen gibt es meistens nur zwei Zustände. Eben
dieses tot oder lebendig, ominöse Begriffe wie halbtot entziehen sich
der wissenschaftlichen Definition und sind daher für eine Simulation
nicht relevant. Die Zustandsmenge, die eine Zelle im Automaten haben kann,
wird mit der Variable k umschrieben. So kann zum Beispiel ein Automat mit
N verschiedenen Zellen Nk verschiedene Muster bilden. Durch die verschiedenen
Regeln, kann ein Automat aber auch unfähig sein, diese Vielfalt von
Zuständen im Verlaufe der Zeit einzunehmen.
Diese unerreichbaren Zustände nennt der Fachmann "Garten-Eden-Zustände"
oder "Paradies-Zustände". Der Mensch träumt auch vom Garten Eden,
ohne ihn jemals zu erreichen, genauso ergeht es dem jeweiligen Automaten.
Die Entwicklungsregeln sind das A und O beim Simulieren mit zellulären
Automaten. Von ihnen hängt es ab, ob die Darstellung des Wachstumsprozesses
gelingt oder nicht.
Das Wichtigste bei den Regeln ist, dass alle Zellen die gleichen Informationen
beinhalten, wie im menschlichen Körper jede Zelle die gleichen DNA-Stränge
aufweist. Die Regeln handeln nur von der einzelnen Zelle und ihrer lokalen
Nachbarschaft, alles was dahinter liegt, wird ignoriert. Die Nachbarschaft
wird beim Erschaffen des Gitters festgelegt.
Die Anzahl möglicher Regeln eines Automaten hängt direkt
von der Zustandsmenge der Zellen und der Größe der Nachbarschaft
ab. Wenn auf einer eindimensionalen Gitterkonstruktion eine Zelle zwei
Zustände einnehmen kann und der Nachbarschaftsradius r = 1 beträgt,
gibt es genau 23 = 8 Möglichkeiten wie die Zustände
in der Nachbarschaft verteilt sein können. Im nächsten Zeitakt
kann jede Zelle entweder den Zustand 0 oder 1 erhalten. Daraus können
wir schließen, dass dieser Automat 28 = 256 mögliche
Spielregelkombinationen besitzt. Allgemein formuliert, kann ein Automat,
in welchem die Zellen k Zustände einnehmen können und sich n
Zellen in der Nachbarschaft befinden, k hoch k hoch n verschiedene Regeln
haben.
Diese Regeln können wir auf verschiedenste Weise formulieren.
Am bekanntesten sind die sogenannten totalistischen Regeln. Bei solchen
Regeln wird nur auf die Anzahl lebender und toter Zellen in der Nachbarschaft
Rücksicht genommen.
Nehmen wir einen Automaten an, welcher eine Zelle erschaffen oder am
Leben erhalten kann, wenn die Summe der Nachbarn 2 beträgt. In allen
andern Fällen würde die Zelle absterben oder gar keine entstehen.
In einer Tabelle dargestellt, sähe dies dann so aus:
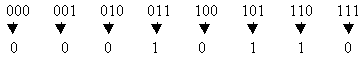
Wenn wir diesen Automaten nun von Hand zeichnen würden, müssten wir prinzipiell vor jedem Zeichenschritt in dieser Tabelle nachlesen und dies dann dementsprechend darstellen. Der PC rechnet ja um einiges schneller.
Es ist für den Computer sinnvoller jedes Mal in einer solchen „look-up-Tabelle“
nachzuschauen als für jede Zelle die Regeln nachzurechnen.
Mathematisch formuliert würde die obige Tabelle zirka so aussehen:
zi(t+1) = {1, wenn (zi-1(t) + zi(t) + zi+1(t)) = 2; 0, sonst}
Wir sehen ein, dass die obige Regel sehr unscheinbar aussieht. Zur graphischen Darstellung verwenden wir ein Programm, welches die einzelnen Ketten des eindimensionalen Automaten direkt untereinander legt. Die Ausgangsposition der einzelnen Zellen ist rein zufällig gewählt. Unsere schlichte Formel sieht dann auf dem Bildschirm nach ca. 47 Rechenschritten aus, wie in Bild N° 6 dargestellt.

Bild N° 6: Totalistischer Automat
Eine Regel, in welcher nur die Gesamtsumme der lokalen Nachbarn zählt,
aber nicht auf die räumliche Anordnung dieser Rücksicht nimmt,
nennt man totalistische Regel. Lässt man bei den Automaten nur diese
totalistischen Regelwerke zu, beschränkt sich die Anzahl von möglichen
Wachstumsregeln erheblich. Ein eindimensionales Spielfeld mit einem binären,
totalistischen Automaten lässt z.B. nur 16 regeltechnische Möglichkeiten
zu.
Dem Programm LIFE liegt eine außentotalistische Regelgebung zugrunde,
da der Zustand der zu berechnenden Zelle in den Mittelpunkt rutscht.
Im Reich der Regeln gibt es unzählige Möglichkeiten. Man
kann großen Wert auf die räumliche Anordnung der Nachbarn legen
oder den "Zufall" ins Spiel bringen.
Es existiert also eine nahezu unendliche Fülle an Regelmaterial,
um das Universum der zellulären Automaten zu beschreiben. Es ist eine
Illusion, wenn man jede einzelne dieser Regelkombinationen einmal ausrechnen
und archivieren möchte. Schon ein eindimensionaler Automat mit 2 möglichen
Zuständen und einer Nachbarschaft mit Radius r = 2 eröffnet 4294967296
verschiedene Regeln. Man stelle sich die Regelfülle bei einem zweidimensionalen
Automaten vor.
Anschließend wollen wir unser Programm zur Erzeugung digitaler
Muster anfügen.
Option Explicit
Const Anz_Zellen = 100 'Anzahl
Zellen pro Zeile
Const Max_Zeilen = 200
'Maximale Anzahl Zeilen
Const Radius = 3 'Nachbarschaftsradius
'2 Zellketten der Länge Anz_Zellen + je einen Radius auf beiden Seiten
Dim Zeile(-Radius To Anz_Zellen + Radius, 0 To 1) As Byte
'Hilfsvariablen um die alte Kette von der Neuen zu unterscheiden
Dim Alt As Byte, Neu As Byte
Dim CodeNo As Integer 'Codenummer
Dim ZeilenNo As Integer 'Aktuelle Zeile
Dim ZellenNo As Integer 'Aktuelle Zelle
Dim x As Integer
'Hilfsvariable zum Zählen
Dim Sum As Byte
'Summe der lebenden Nachbarn
Dim r(Radius * 2 + 1) As Byte 'Regel
Sub Berechne() 'Hauptroutine
CodeNo = 12 'CodeNummer nach Belieben wählen
Text1.Text = CodeNo
Text1.Refresh
Alles_Neu
'Wandelt die Codenummer im Dezimalsystem in eine binäre Regel um
r(0) = Int(CodeNo / 1) Mod 2
r(1) = Int(CodeNo / 2) Mod 2
r(2) = Int(CodeNo / 4) Mod 2
r(3) = Int(CodeNo / 8) Mod 2
r(4) = Int(CodeNo / 16) Mod 2
r(5) = Int(CodeNo / 32) Mod 2
r(6) = Int(CodeNo / 64) Mod 2
r(7) = Int(CodeNo / 128) Mod 2
For ZeilenNo = 0 To Max_Zeilen 'Für jede Zeile
Alt = Abs(Alt - 1) 'Aus Alt wird Neu
Neu = Abs(Neu - 1) 'Aus Neu wird Alt
For ZellenNo = 0 To Anz_Zellen 'Für jede Zelle
Sum = 0 'Summe zurücksetzen
For x = -Radius To Radius 'Summe ermitteln
Sum = Sum + Zeile(ZellenNo + x, Alt)
Next x
Select Case Sum `Wähle für Summe
Case 0: Zeile(ZellenNo, Neu) = r(0) 'Summe = 0
Case 1: Zeile(ZellenNo, Neu) = r(1) 'Summe = 1
Case 2: Zeile(ZellenNo, Neu) = r(2) 'etc...
Case 3: Zeile(ZellenNo, Neu) = r(3)
Case 4: Zeile(ZellenNo, Neu) = r(4)
Case 5: Zeile(ZellenNo, Neu) = r(5)
Case 6: Zeile(ZellenNo, Neu) = r(6)
Case 7: Zeile(ZellenNo, Neu) = r(7)
End Select
'Zeichnen der Neuen Zelle
Picture1.PSet(ZellenNo, ZeilenNo), RGB(255 * Zeile(ZellenNo, Neu), 255 * Zeile(ZellenNo, Neu), 255 * Zeile(ZellenNo, Neu))
Next ZellenNo 'Nächste Zelle
Next ZeilenNo 'Nächste Zeile
End Sub
Sub Alles_Neu() 'Setzt Alte Variablen zurück
Picture1.Cls 'löscht die Bildschirmanzeige
ZeilenNo = 0
Alt = 0
Neu = 1
For ZellenNo = 0 To Anz_Zellen
Zeile(ZellenNo, Alt) = 0
Zeile(ZellenNo, Neu) = Int(Rnd(1)*2)
'Zufallsbedingungen in Next ZellenNo der ersten Zeile
EndSub
Private Sub CoStart_Click()
'Wenn der Start-Button angeklickt wird
Berechne 'Hauptroutine aufrufen
End Sub
Private Sub Form_Load()
'Am ersten Start des Programms
Alles_Neu
Zufall
End Sub
Jeder Code im Programm verkörpert eine bestimmte Regelfolge. Diese Folgen errechnet der Computer aus der Codenummerierung. Wir gehen an dieser Stelle nicht näher auf diese Codes ein.
Wie in der Geschichte der zellulären Automaten schon erwähnt,
machte sich Stephen Wolfram dahinter, Ordnung im Chaos dieser Regeln zu
schaffen.
Er beschränkte seine Katalogisierung auf totalistische, legale
eindimensionale Automaten. D.h. auf Automaten, die nur auf die Gesamtsumme
von Zellen in der Nachbarschaft, nicht aber deren Anordnung reagieren und
in denen aus einem absoluten Nullstand der Zellen keine neuen entstehen
können.
Nach Abertausenden von Computerberechnungen fanden er und seine Mitarbeiter
heraus, dass man die eindimensionalen Automaten in 4 Klassen unterteilen
kann.
Nach reiflicher Überlegung wurde die Klassifizierung auch auf
zwei- und dreidimensionale Automaten übertragen.
Seine Klassen umfassten folgende Kriterien:
- In der ersten Klasse befinden sich alle Automaten, die sich aus allen möglichen Anfangszuständen zu einem unveränderlichen Endstand entwickeln. Es ergeben sich sehr monotone Gebilde.
- Zweitklassig sind alle Automaten, welche periodische Muster ausbilden.
Anders als in der ersten Klasse überleben nur einzelne mehr oder weniger breite Stränge von Zellen. Diese sehen am Schluss wie ein Strichcode aus. - Chaotisch und unvorhersehbare Strukturen zeigt die dritte Automatenklasse auf. Es sind in dieser Klasse nur noch Strukturoasen machbar, die Struktur erstreckt sich über den gesamten Bildschirm. Diese Klasse kommt am häufigsten vor.
- Die seltenen Exemplare der vierten Klasse bilden komplizierte, voneinander räumlich getrennte Strukturen, welche sich ähnlich einem Gleiter in LIFE, durch Raum und Zeit fortbewegen. Diese Strukturen sind auch mit höchster Anstrengung nicht vorhersagbar. Die vierte Klasse verkörpert den Rand des Chaos.
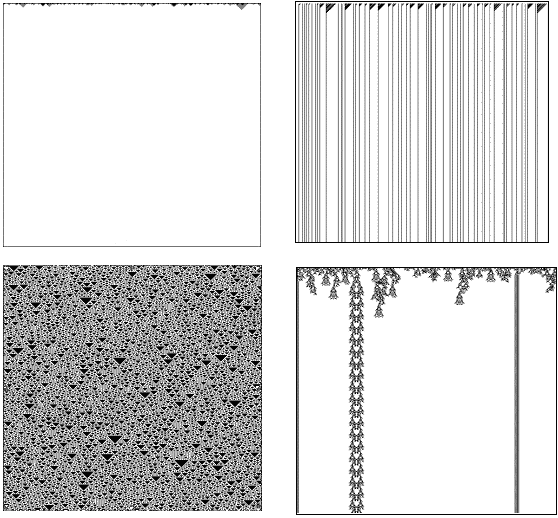
Bild N° 7: Die vier Klassen der Automaten
Ein Wissenschaftler namens Christopher Langton fand heraus, wie man
einen Automaten nur nach seiner Produktionsregel in eine der Klassen einteilen
kann.
Er entwickelte den Parameter λ (Lambda).
Dieser Parameter drückt die Wahrscheinlichkeit aus, mit welcher
ein Punkt in der nächsten Runde überlebt oder nicht. Uns war
es leider nur möglich, die Wahrscheinlichkeit der ersten Zeile zu
berechnen. Wir haben uns aus diesem Grund für ein mehr brachiales
Verfahren entschieden. Es ist ein experimentelles Herumknobeln mit dem
PC. So kommen wir zwar zur richtigen Lösung, aber der Weg steht im
Widerspruch zu unserer Vorstellung von einer korrekten mathematischen Antwort.
Langton fand heraus, dass Automaten mit λ = 0 erstklassigen Ursprungs sind, da alles Leben hier sofort ausstirbt, gleich wie bei der Wahrscheinlichkeit λ = 1, nur dass da alles am Leben ist.
Automaten der dritten Klasse tauchen vor allem bei einer Wahrscheinlichkeit
von etwa 0,5 auf. Hier durchlebt der Automat ein großes Wirrwarr
von toten und lebendigen Zellen. Als er einige dieser Meilensteine setzen
konnte, widmete er sich der Erforschung der Wahrscheinlichkeiten zwischen
0 und 0,5 bzw. 0,5 und 1 (Hier sind einfach die Werte tot und lebendig
vertauscht). Zwischen dem Bereich 0 und 0,3 sind die Automaten der zweiten
Klasse definiert. Die magische Schwelle befindet sich etwa bei 0,3, hier
taucht man ein ins Reich der viertklassigen Automaten.
Durch diesen Parameter ist es um einiges einfacher die Automaten den
Klassen zuzuordnen.
Zusammenfassend lässt sich also sagen, das die Zellulären
Automaten im Prinzip die Regeln der Zivilisation, des Universums oder des
Lebens im Kleinen ausdrücken und verkörpern.
Ein recht spezieller, zweidimensionaler Automat, der hier nicht fehlen darf, ist die sogenannte "Misch-Masch-Maschine". Es handelt sich dabei um die Simulation der cAMP Wellen, bzw. Belousov-Zhabotinsky Reaktion, mit der Zustandsentwicklung
![zij(t+1) = [Kij(t)/k1] + [Iij(t)/k2] zij(t+1) = [Kij(t)/k1] + [Iij(t)/k2]](lsyspics/fkt_f01.gif) wenn zij = 0
wenn zij = 0
![zij(t+1) = [(Summe zkl(t) von 0<zkl(t)<V bis (k,l)Element Nij)/Iij(t)] + g zij(t+1) = [(Summe zkl(t) von 0<zkl(t)<V bis (k,l)Element Nij)/Iij(t)] + g](lsyspics/fkt_f02.gif) wenn 0 < zij(t) < V
wenn 0 < zij(t) < V
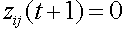 wenn zij = V
wenn zij = V
Dabei werden alle Zellen K genannt, deren Zustand gleich V ist. Alle
übrigen Zellen werden I genannt.
k1, k2, g und V sind Parameter. k1
und k2 geben die Reizschwelle für den ersten Rezeptor an,
V die Reizschwelle für den zweiten Rezeptor g entspricht der cAMP
Produktionsmenge. Die Randbedingungen sind beliebig wählbar.
Das Prinzip des Automaten ist denkbar einfach: Jede Zelle passt sich
dem Grad der Infektion ihrer relativen Nachbarn an und erhöht ihn
um ein Quantum g. Ist eine maximale Infektionsstärke erreicht, fällt
der Infektionsgrad auf Null zurück.