Zelluläre Automaten - Bakterien
Ablagerungen und Anlagerungen
Ab-, bzw. Anlagerung ist die einfachste denkbare Wachstumsform. Biologische,
chemische sowie rein physikalische Prozesse können als Ablagerungswachstum
bezeichnet werden. Ein Objekt wächst dabei nicht unbedingt aus "eigener"
Kraft, sondern übernimmt die Elemente, aus denen es besteht, direkt
aus seiner Umgebung ohne sie gezielt zu verändern.
Einmal bestehende Elemente eines Objekts bleiben wie und wo sie sind.
Damit ist das Hauptprinzip des Wachstums durch An- und Ablagerung charakterisiert.
Betrachten wir ein Glas Wasser, in das wir einen Löffel Sand und
Erde gegeben haben. Jedes Sedimentkörnchen, das auf dem Grund des
Gefäßes angekommen ist, bleibt unweigerlich dort. Auf dem Boden
wächst langsam eine lockere Schicht Schlamm, die oberen Lagen stützen
sich auf den unteren ab.
Den gleichen Effekt können wir bei Korallenriffen beobachten:
Auf dem Meeresgrund wächst eine Schicht Korallen heran. Bald wachsen
andere Korallen darüber und die unteren Lagen sterben ab. Aber das
Kalkgerüst bleibt als Basis für die oberen Schichten bestehen.
Die Kristallisation folgt denselben Regeln: Freie Moleküle in
einer Lösung (z.B. Salz in Wasser) fügen sich an einem Punkt
des bestehenden Kristalls an und bieten damit Fläche für neue
freie Moleküle.
Wie aber können drei Wachstumsvorgänge mit ein und dem selben
Konstruktionsprinzip drei derart verschiedene Endformen hervorbringen?
Diese Frage werden wir beantworten.
Kehren wir noch einmal zum Wasserglas zurück: Welche Komponenten treten in diesem Gedankenexperiment auf?
- Der Teil "Ablagerungen und Anlagerungen" handelt von Wachstumsformen, die durch stetiges Anfügen von Bausteinen entstehen. So zum Beispiel Kristalle und Eisblumen, aber auch Korallen. Mit mehreren chemischen Experimenten sowie einer ersten Computersimulation erzielen wir analoge Ergebnisse.
- In "Wachstum und Ausbreitung von Bakterien und niederen Pilzen" geht es um die relativ instabilen Wachstumsmuster einzelliger Lebewesen. Überlebenskampf, Selektion und Mutation stehen im Zentrum.
- Von der Petrischale an den Bildschirm: Der zelluläre Automat ist ein wahres Wunderwerkzeug mit einem sehr breiten Anwendungsspektrum. Wir betrachten zuerst seine Funktionsweise und leuchten auch den geschichtlichen Hintergrund aus.
- Im Abschnitt Krieg der Kulturen wagen wir den interessanten Versuch Zelluläre Automaten gegeneinander kämpfen zu lassen. Die Resultate überraschen!
- Noch praxisnäher geht es im letzten Abschnitt zu, wo wir versuchen den "Krieg der Kulturen" mit Elementen der Populationsdynamik zu verknüpfen.
Mit diesen Fakten können wir bereits ein erstes, einfaches Computerprogramm
schreiben, das die Zufallsanlagerung an einen Punkt simuliert. Zuerst definieren
wir ein Spielfeld in Form einer Matrix mit festen Grenzen (z.B. 400 * 400
Punkte), und einen maximalen Radius Max_Radius,
den die Figur erreichen soll (mit Vorteil den halben Matrixdurchmesser, also 200).
Auf jedem Punkt dieser Matrix kann eine Ganzzahl von 0 bis 255 stehen.
Es gelten folgende Definitionen:
- 0 Leer
- 1 Ein besetzter Nachbar
- 2 Zwei besetzte Nachbarn
- ... ...
- 8 Acht besetzte Nachbarn
- 10 Besetzt
- 99 Außerhalb
Außerdem definieren wir einen Parameter Radius, der die aktuelle Größe der Figur angibt.
Dann nehmen wir einen Startpunkt in der Mitte auf unserem Spielfeld an, d.h. wir weisen ihm den Wert 10 für "Besetzt" und den anliegenden Punkten den Wert 1 für "Ein besetzter Nachbar" zu. Es könnten auch mehrere Startpunkte angenommen werden. Allen Punkten, die mehr als Radius + 10 Einheiten vom Startpunkt entfernt sind, weisen wir den Wert 99 für "Außerhalb" zu.
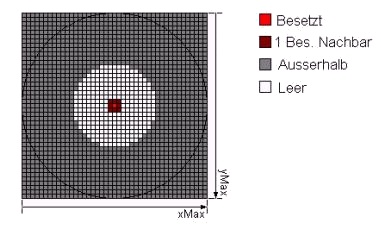
Bild N° 1: Matrix
Sobald die Matrix derart präpariert ist, lassen wir einen
Punkt einen zufälligen Weg von der Grenze zwischen Leer und Außerhalb
(Kreis(M, Radius)) aus über den Bildschirm "wandern", in dem wir ein
Koordinatenpaar (xWander, yWander) zufällig
manipulieren. Trifft der wandernde Punkt an einen besetzten Punkt, so wird
er an der Seite, an der er den Punkt getroffen hat, mit einer gewissen
Wahrscheinlichkeit angelagert, d.h. ebenfalls zu einem besetzten Punkt.
Ist das geschehen, so nehmen wir einen neuen Wanderpunkt an und so weiter...
(Bild N° 2). Dabei ist nicht zu vergessen, den Parameter Radius
laufend der Größe der Figur anzupassen und dementsprechend die
Grenze Außerhalb / Leer weiter zu ziehen.
Den ganzen Vorgang wiederholen wir solange, bis der Radius der Figur
unseren Wünschen, d.h. dem Wert Max_Radius
entspricht.

Bild N° 2
Bevor wir zu den Ergebnissen kommen, geben wir hier das Programm wieder. Zuerst in einem Algorithmenschema (Flussdiagramm), dann im Volltext. Um das Programm zu testen, sind zwei Grafikelemente notwendig: Einen Command-Button mit dem Namen “CoStart“ und ein Bildfeld mit dem Namen “Picture1“, das mindestens 200 * 200 Bildpunkte groß ist.
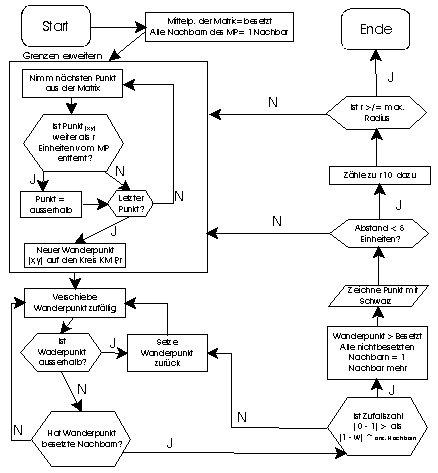
'Allgemeine Definitionen
Const pi = 3.1415965357
Dim x As Integer, y As Integer 'Koordinaten
'Matrixdefinitionen
Const xMax = 200, yMax = 200
'Randbegrenzung
Const Max_Radius = 100
'Maximaler Radius
Dim Punkt(-5 To xMax + 5, -5 To yMax + 5)
As Byte 'Matrix mit"Reserverand"
'Graphik
Const Wahrscheinlichkeit = 1
'Wahrscheinlichkeit, mit der ein Punkt angelagert wird.
Const Leer = 0 'Feldzustände
'Zustände 1 bis 8 für Anz. schwarze Nachbarn
Const Schwarz = 10, Aussen = 99
Dim Radius As Integer 'Aktueller Radius
Dim xWander As Integer , yWander As Integer 'Wander- Punkt Koordinaten
'Wege
Dim Wx(0 To 7) As Integer 'Möglichkeiten der x-Verschiebung
Dim Wy(0 To 7) As Integer 'Möglichkeiten der y-Verschiebung
Dim n As Byte 'Zähler für Verschiebungen
Sub Graphik()
'Matrix präparieren
Punkt(Max_Radius, Max_Radius)= Schwarz 'Fixpunkt setzen
For n = 0 To 7
Punkt(Max_Radius + Wx(n), Max_Radius + Wy(n)) = 1
'...Nachbar
Next n
Picture1.PSet(Max_Radius, Max_Radius), RGB(0, 0, 0)
For x = -5 To xMax + 5 'Randbegrenzungen und Nachbarn
For y = -5 To yMax + 5
If Sqr((x - Max_Radius) ^ 2 + (y - Max_Radius) ^ 2) > Radius + 10 Then Punkt(x, y) = Aussen
Next y
Next x
'Hauptschleife
Do While Radius + 10 <= Max_Radius
'Wiederhole bis Max_Radius
'Wander-Punkt zufällig auf dem Kreis mit r = Radius Wählen
xWander = Cos(Rnd(1) * 2 * pi) * (Radius + 10) + Max_Radius
yWander = Sin(Rnd(0) * 2 * pi) * (Radius + 10) + Max_Radius
100 'Aktuelle Position zufällig in eine von 8 Richtungen verschieben
xWander = xWander + Wx(Int(Rnd(1) * 8))
yWander = yWander + Wy(Int(Rnd(0) * 8))
'Kontrollieren der Randbegrenzungen
If Punkt(xWander, yWander) = Aussen Or Punkt(xWander,yWander) = Schwarz Then
xWander = xWander - Wx(Int(Rnd(0) * 8))
yWander = yWander - Wy(Int(Rnd(0) * 8))
End If
'Versuchen neuen Punkt anzulagern falls schwarzer Nachbar
If Not Punkt(xWander, yWander) = Leer
And Punkt(xWander, yWander) < Schwarz
And Rnd(1) > (1 - Wahrscheinlichkeit) ^ Punkt(xWander, yWander) Then Punkt(xWander, yWander) = Schwarz
Picture1.PSet(xWander, yWander), RGB(0, 0,0)
For n = 0 To 7
If Not Punkt(xWander + Wx(n), yWander + Wy(n)) = Schwarz
Then Punkt(xWander + Wx(n), yWander + Wy(n)) = Punkt(xWander + Wx(n), yWander + Wy(n)) + 1
Next n
GoTo 200 'Neuer Punkt
Else
GoTo 100 'Kein neuer Punkt
End If
200 'Randbegrenzungen erweitern falls nötig
If Sqr ((xWander - Max_Radius) ^ 2 + (yWander - Max_Radius) ^ 2) > Radius + 5 Then
Radius = Sqr((xWander - Max_Radius) ^ 2 + (yWander - Max_Radius) ^ 2)
For x = Max_Radius - Radius - 10 To Max_Radius + Radius + 10
For y = Max_Radius - Radius - 10 To Max_Radius + Radius + 10
If Sqr((x - Max_Radius) ^ 2 + (y - Max_Radius)
^ 2) < Radius + 10 And Punkt(x, y) = Aussen Then Punkt(x, y) = Leer
Next y
Next x
End If
Loop
End Sub
Private Sub CoStart_Click()
Wx(0) = 1: Wy(0) = 1 'Wege definieren
Wx(1) = 0: Wy(1) = 1
Wx(2) = -1: Wy(2) = 1
Wx(3) = 1: Wy(3) = 0
Wx(4) = -1: Wy(4) = 0
Wx(5) = 1: Wy(5) = -1
Wx(6) = 0: Wy(6) = -1
Wx(7) = -1: Wy(7) = -1
Zufall
Graphik
End Sub
Folgende Ausgaben (Bild N° 3a, 3b, 3c) erhalten wir mit genau den vorgeschlagenen Parametern. Die Punkte sind nach dem Zeitpunkt ihrer Anlagerung eingefärbt. Man kann sehr gut eine Verzweigungsstruktur erkennen, die wir nun etwas genauer untersuchen wollen.



Bild N° 3 a) - c) Anlagerung mit den Parametern w=1, w=0,1 bzw. w=0,01
Wie kommt eine solche Struktur überhaupt zustande? Warum haben
wir nicht einfach einen formlosen Klumpen sondern sehr organisch wirkende
Muster auf unserem Bildschirm?
Eine einfache Überlegung lüftet das Geheimnis: Die Spitzen
wachsen schneller als der Rest, weil die Wahrscheinlichkeit weit größer
ist, dass ein Punkt sich zuäußerst anlagert als dass er sich
bis nach ganz innen durchmanövriert.
Wir können die Wahrscheinlichkeit, mit der ein neuer Punkt an einem bestimmten Ort angelagert wird, experimentell ermitteln: Zuerst halten wir das Wachstum der Figur an, indem wir die Zeile
Punkt(xAlt, yAlt)= Besetzt
'Punkt in der Matrix auf Besetzt setzen
löschen. Dann zählen wir mit einer zusätzlichen Variable,
wie oft der Wander-Punkt an diesem Ort ankommt. Je öfter er das tut,
desto größer ist die Wahrscheinlichkeit, dass sich an dieser
Stelle ein Punkt anlagert.
Wir haben für das folgende Bild (N° 4 a) sämtliche Punkte
- mit einer beträchtlichen Menge an Rechenaufwand - analysiert. Punkte
mit der gleichen Wahrscheinlichkeit wurden mit derselben Farbe gekennzeichnet.
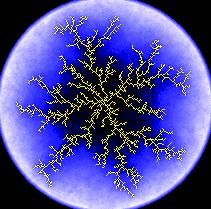

Bild N° 4a) Experimentelle Ermittlung, Bild N° 4b) Rechnerische Ermittlung
Mit diesem experimentellen Verfahren kann ein zwar richtiges, aber nur
sehr schlecht erkennbares Resultat erreicht werden. Wir haben ein weiteres,
rein rechnerisches Verfahren angewandt, das ein weitaus zufriedenstellenderes
Ergebnis liefert: Bild N° 4 b). Die Grenzen zwischen den Streifen sind
die Äquipotentiallinien der Figur. Auf einer Äquipotentiallinie
ist die Wahrscheinlichkeit, dass sich ein Punkt anlagert, überall
gleich groß. Jeden Streifen nach innen sinkt die Wahrscheinlichkeit
um 90%, also sehr schnell.
Eine weitere Analyse, die wir am selben Bild durchführen wollen,
ist die sogenannte Horton-Analyse. Wir klassifizieren die Äste in
Hauptäste (Ordnung 1), Nebenäste (Ordnung 2), Nebennebenäste
(Ordnung 3), etc. Dann vergleichen wir die Anzahl und die Größe
der Äste der verschiedenen Ordnungen.
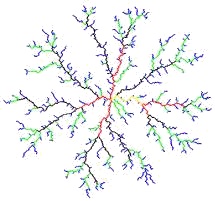
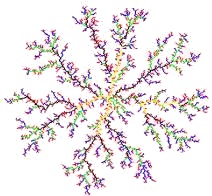
Bild N° 5a) und 5b) Horton-Analyse
Für die Horton-Analyse eignen sich nur Bilder mit w ≈ 1, da bei den anderen keine klaren Verzweigungen zu erkennen sind. Die Anzahl der Äste wächst mit jeder Unterordnung etwa um den Faktor 5. Ihre durchschnittliche Länge nimmt dabei um ca. 10/27 ab. Damit steigt die Gesamtmasse jeder Ordnung um 185 %.
Als letzte Analyse wollen wir die fraktale Dimension des Gebildes ermitteln und diese in Relation mit dem Parameter w stellen. Den Begriff der fraktalen Dimension erklären wir im nachfolgenden Exkurs.
Exkurs N° 6: Fraktale Dimension
Für unsere Figur hieße das nun, dass
ihre fraktale Dimension für den Parameter w = 1 berechnet wird zu 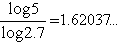
Mit einer anderen Methode1 haben wir auch die fraktale Dimension für andere w untersucht. Dabei zeigt sich folgende Abhängigkeit:
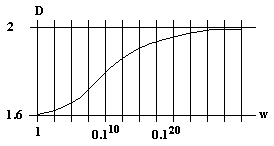
Eine Reihe von Naturvorgängen zeigen das gleiche Wachstumsprinzip.
Wir können den natülichen Formen mit denselben Mitteln eine
fraktale Dimension und mit Hilfe der obigen Funktion einen Parameter w
zuordnen. Dies könnte z.B. als Klassifikationshilfe dienen oder als
Hinweis auf physikalische Eigenschaften.
Die im Exkurs vorgestellten Zinksulfaltblättchen weisen eine fraktale
Dimension von 1.87 auf. Wir folgern daraus, dass sich ein freies Zinkatom
mit der Wahrscheinlichkeit w = 1·10-13 an die bestehende
Figur anlagert.
1Es handelt sich dabei um die sogenannte Box-Count-Methode. Siehe Michael F. Barnsley: "Fractals Everywhere", S.197. [zurück]
Exkurs N° 7: Zinksulfat Experiment