Fraktale Dimension [Exkurs 6]
>> Die Mathematiker mussten während ihrer Krise in den Jahren 1875 bis 1925 erkennen, dass ein genaues Verständnis von Irregularität und Zersplitterung (ebenso wie von Regularität und Zusammenhang) nicht dadurch erreicht werden kann, dass man die Dimensionen als Anzahl der Koordinaten definiert.<<1
1Aus B.B. Mandelbrot: "Die fraktale Geometrie der Natur" S. 26 a)

Aus einem gegebenen Einheitsintervall wird das mittlere Drittel entfernt.
Es bleiben das erste und dritte Drittel. Aus diesen zwei Dritteln wird
nun wiederum der mittlere Teil entfernt, usw. Was bleibt ist schließlich
eine unendliche Menge unendlich kleiner Intervalle; also unendlich viele
Punkte. Diese Punkte werden Cantor-Menge genannt.
Die Gesamtstrecke aller verbleibenden Punkte ist 0, da die einzelnen
Punkte keine Länge haben. Die Cantor-Menge hat also nach Euklid keinen
Wert in der zweiten Dimension. Ebenfalls kann sie nach Euklid auch nicht
in der ersten Dimension definiert werden, da die Anzahl der Punkte unendlich
ist. Wir brauchen also eine nichteuklidische Dimension, irgendwo zwischen
0 und 1. Cantor errechnete diese folgendermaßen:
Nach dem ersten Schritt ist die Gesamtlänge des Intervalls 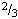 . Nach dem zweiten Schritt
. Nach dem zweiten Schritt 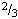 mal
mal 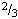 oder
oder 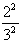 .
Nach n Schritten beträgt die Länge noch
.
Nach n Schritten beträgt die Länge noch 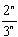 und nach unendlich vielen Schritten noch
und nach unendlich vielen Schritten noch 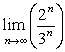 .
.
Wir logarithmieren 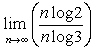 und kürzen
und kürzen 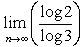 .
.
Damit ist die fraktale Dimension der Cantor-Menge 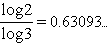 .
.